Saat kelas X, Anda tentu sudah mengenal istilah perpindahan.
Perpindahan dapat diartikan sebagai perubahan posisi suatu partikel.
Misalnya:
Andi mengendarai mobil ke arah barat sejauh 3 m. Kemudian, ia berbelok ke arah utara sejauh 4 m. Gambarlah perpindahan posisi Andi sekarang!
Permasalahan tersebut dapat diselesaikan dengan cara berikut:
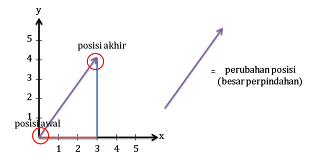
Pada mulanya, mobil Andi berada pada titik pusat koordinat (posisi awal). Lalu, mobil tersebut melaju ke barat sejauh 3 m (garis merah). Kemudian, berbelok ke utara sejauh 4 m (garis biru) lalu berhenti (posisi akhir).
Cara menentukan perpindahannya adalah dengan menarik garis dari posisi awal sampai posisi akhir.
Lihatlah gambar di bawah ini!
$\textup{Terdapat 2 buah posisi, yaitu: } \vec{r_{1}} \textup{ dan } \vec{r_{2}}$
$\Delta\vec{r} = \textup{perpindahan posisi}$
Lalu, masih ingatkah Anda tentang penjumlahan vektor?
$\vec{r_{1}}+ \Delta\vec{r}= \vec{r_{2}}$
$\Delta\vec{r} = \vec{r_{2}}- \vec{r_{1}}$
Sehingga, kita mendapat rumus perpindahan posisi, yaitu:
$\Delta\vec{r} = \vec{r_{2}}- \vec{r_{1}}$
Setiap posisi memiliki koordinat-nya tersendiri yang dapat diubah dalam vektor satuan.
$\vec{r}= xi + yj$
$\vec{r_{1}}= x_{1}i + y_{1}j$
$\vec{r_{2}}= x_{2}i + y_{2}j$
$\textup{Jika } \vec{r_{1}} \textup{ dan} \vec{r_{2}} \textup{ dimasukkan ke dalam rumus perpindahan posisi maka:}$
$\Delta\vec{r} = \vec{r_{2}}- \vec{r_{1}}$
$\Delta\vec{r} = x_{2}i + y_{2}j - (x_{1}i + y_{1}j)$
$\Delta\vec{r} = x_{2}i + y_{2}j -x_{1}i -y_{1}j$
$\Delta\vec{r} = x_{2}i - x_{1}i + y_{2}j - y_{1}j$
$\Delta\vec{r} = (x_{2} - x_{1})i + (y_{2}- y_{1})j$
Rumus diatas merupakan cara mencari vektor perpindahan.
$\textup{INGATLAH!}$
$\textup{Setiap vektor satuan } xi + yj \textup{ memiliki besar } \sqrt{x^{2}+y^{2}}$
$\textup{sehingga:}$
$\textup{sehingga:}$
$s \textup{ (besar perpindahan)} = \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$
Berarti, kita mendapat 3 rumus, yaitu:
$\Delta\vec{r} = \vec{r_{2}}- \vec{r_{1}}$
$\Delta\vec{r} = (x_{2} - x_{1})i + (y_{2}- y_{1})j \textup{*}$
$s = \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\textup{*}$
*rumus yang sering dipakai
Contoh soal 1:
a. vektor satuan dari masing-masing posisi
b. vektor perpindahannya
b. vektor perpindahannya
c. besar perpindahannya
Pembahasan soal 1:
a. Vektor satuan: xi + yj
Koordinat (1, 3) memiliki vektor satuan i + 3j
Koordinat (3,1) memiliki vektor satuan 3i + j
b. Vektor perpindahan:
$\Delta\vec{r} = (x_{2} - x_{1})i + (y_{2}- y_{1})j$
$\Delta\vec{r} = (3 - 1)i + (1 - 3)j$
$\Delta\vec{r} = 2i - 2j$
c. Besar perpindahan:
$s = \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$
$s = \sqrt{(2)^{2}+(-2)^{2}}$
$s = \sqrt{8}$
$\mathbf{s = 2\sqrt{2} \textup{ m}}$
Mungkin Anda bertanya-tanya mengapa vektor perpindahannya adalah 2i-2j padahal di gambar (gambar di contoh soal) tidak tampak seperti itu.
Untuk membuktikan kebenaran tersebut, vektor perpindahan tersebut harus dipindahkan ke titik sumbu koordinat, seperti di bawah ini:

Gambar di samping membuktikan bahwa vektor perpindahan tersebut memang 2i - 2j (2,-2).
Dapat disimpulkan, perpindahan juga merupakan vektor, oleh karena itu berlaku rumus berikut:
1. Sumbu x vektor perpindahan:**
$s_{x} = \textup{s } cos\ \theta$
2. Sumbu y vektor perpindahan:**
$s_{y} = \textup{s } sin\ \theta$
3. Arah perpindahan:
$\tan \theta = \frac{s_{y}}{s_{x}}$
Hal ini juga berlaku untuk vektor posisi:
1. Sumbu x vektor posisi:**
$r_{x} = \textup{r } cos\ \theta$
2. Sumbu y vektor posisi:**
$r_{y} = \textup{r } sin\ \theta$
3. Arah vektor posisi:
$\tan \theta = \frac{r_{y}}{r_{x}}$
Catatan:
**Rumus no.1 dan no.2 berguna untuk pengerjaan soal seperti mengenai arah mata angin.
Daftar besar sudut arah mata angin:

Timur (T) = 0* (x = + y = 0)
Timur Laut (TL) = 45* (x = + y = +)
Utara (U) = 90* (x = 0 y = +)
Barat Laut (BL) = 135* (180-45) (x = + y = -)
Barat (B) = 180* (180 - 90) (x = - y = 0)
Barat Daya (BD) = 225* (180+45) (x = - y = -)
Selatan (S) = 270* (180+90) (x = 0 y = -)
Tenggara (TG) = 315* (360-45) (x = + y = -)
*dalam derajat
Contoh soal 2:
$\textup{Sebuah mobil melaju dan menempuh 3 km ke barat dan kemudian menempuh } 4 \sqrt{2} \textup{ km ke arah tenggara}$
$\textup {dan akhirnya 3 km ke utara. Tentukan besar dan arah perpindahan mobil terhadap titik berangkatnya!}$
Pembahasan soal 2:
///////////////////////////////////////////////////////besar perpindahan////////////////////////////////////////////////
Pertama-tama kita harus tentukan dulu masing-masing vektor posisi dalam vektor satuan:
Catatan:
**Bagi vektor yang horizontal atau vertikal tidak perlu memakai rumus no.1 dan no.2, sedangkan vektor yang miring harus memakai rumus no.1 dan no.2
1. Posisi 1 ke arah barat 3 m, berarti x = -3 y = 0 (lihat daftar)
$\vec{r_{1}} = -3i + 0y$
$\vec{r_{1}} = -3i$
2. Posisi 2 ke arah tenggara, berarti:
$r_{2x} = \textup{r } cos\ \theta$
$r_{2x} = (4\sqrt{2}) (cos\ \315^{\circ})$
$r_{2x} = (4\sqrt{2}) (\frac {1} {2} \sqrt{2})$
$r_{2x} = 4$
$r_{2y} = \textup{r } sin\ \theta$
$r_{2y} = \textup{4 } sin\ \315^{\circ}$
$r_{2y} = (4\sqrt{2}) (- \frac {1} {2} \sqrt{2})$
$r_{2y} = -4$
$\vec{r_{2}} = 4i - 4j$
3. Posisi 3 ke arah utara 3 m, berarti x = 0 y = 3:
$\vec{r_{3}} = 3j$
Gambar di atas adalah gambar seluruh vektor posisi yang terdapat dalam soal. Sesuai gambar, berlaku:
$\Delta r = \vec{r_{1}}+ \vec{r_{2}}+ \vec{r_{3}}$
$\Delta r = -3i + 4i - 4j + 3j$
$\Delta r = (-3+4)i + (-4+3)j$
$\Delta r = i - j$
Maka besar perpindahan adalah:
$s = \sqrt{(\Delta r_{x})^{2}+(\Delta r_{y})^{2}}$
$s = \sqrt{1^{2} + (-1)^{2}}$
$\mathbf{s = \sqrt {2} \textup{ km}}$
///////////////////////////////////////////////////////arah perpindahan////////////////////////////////////////////////
Tinggal memakai rumus no. 3:
$\tan \theta = \frac{\Delta r_{y}}{\Delta r_{x}}$
$\tan \theta = \frac{1}{-1}$
$\tan \theta = -1$
$\mathbf {\theta = 315^{\circ}} \textup{(KUADRAN IV [360-45] karena x negatif)}$
Jangan lupa tinggalkan komen! ^_^
Mungkin Anda bertanya-tanya mengapa vektor perpindahannya adalah 2i-2j padahal di gambar (gambar di contoh soal) tidak tampak seperti itu.
Untuk membuktikan kebenaran tersebut, vektor perpindahan tersebut harus dipindahkan ke titik sumbu koordinat, seperti di bawah ini:

Gambar di samping membuktikan bahwa vektor perpindahan tersebut memang 2i - 2j (2,-2).
Dapat disimpulkan, perpindahan juga merupakan vektor, oleh karena itu berlaku rumus berikut:
1. Sumbu x vektor perpindahan:**
$s_{x} = \textup{s } cos\ \theta$
2. Sumbu y vektor perpindahan:**
$s_{y} = \textup{s } sin\ \theta$
3. Arah perpindahan:
$\tan \theta = \frac{s_{y}}{s_{x}}$
Hal ini juga berlaku untuk vektor posisi:
1. Sumbu x vektor posisi:**
$r_{x} = \textup{r } cos\ \theta$
2. Sumbu y vektor posisi:**
$r_{y} = \textup{r } sin\ \theta$
3. Arah vektor posisi:
$\tan \theta = \frac{r_{y}}{r_{x}}$
Catatan:
**Rumus no.1 dan no.2 berguna untuk pengerjaan soal seperti mengenai arah mata angin.
Daftar besar sudut arah mata angin:

Timur (T) = 0* (x = + y = 0)
Timur Laut (TL) = 45* (x = + y = +)
Utara (U) = 90* (x = 0 y = +)
Barat Laut (BL) = 135* (180-45) (x = + y = -)
Barat (B) = 180* (180 - 90) (x = - y = 0)
Barat Daya (BD) = 225* (180+45) (x = - y = -)
Selatan (S) = 270* (180+90) (x = 0 y = -)
Tenggara (TG) = 315* (360-45) (x = + y = -)
*dalam derajat
Contoh soal 2:
$\textup{Sebuah mobil melaju dan menempuh 3 km ke barat dan kemudian menempuh } 4 \sqrt{2} \textup{ km ke arah tenggara}$
$\textup {dan akhirnya 3 km ke utara. Tentukan besar dan arah perpindahan mobil terhadap titik berangkatnya!}$
Pembahasan soal 2:
///////////////////////////////////////////////////////besar perpindahan////////////////////////////////////////////////
Pertama-tama kita harus tentukan dulu masing-masing vektor posisi dalam vektor satuan:
Catatan:
**Bagi vektor yang horizontal atau vertikal tidak perlu memakai rumus no.1 dan no.2, sedangkan vektor yang miring harus memakai rumus no.1 dan no.2
1. Posisi 1 ke arah barat 3 m, berarti x = -3 y = 0 (lihat daftar)
$\vec{r_{1}} = -3i + 0y$
$\vec{r_{1}} = -3i$
2. Posisi 2 ke arah tenggara, berarti:
$r_{2x} = \textup{r } cos\ \theta$
$r_{2x} = (4\sqrt{2}) (cos\ \315^{\circ})$
$r_{2x} = (4\sqrt{2}) (\frac {1} {2} \sqrt{2})$
$r_{2x} = 4$
$r_{2y} = \textup{r } sin\ \theta$
$r_{2y} = \textup{4 } sin\ \315^{\circ}$
$r_{2y} = (4\sqrt{2}) (- \frac {1} {2} \sqrt{2})$
$r_{2y} = -4$
$\vec{r_{2}} = 4i - 4j$
3. Posisi 3 ke arah utara 3 m, berarti x = 0 y = 3:
$\vec{r_{3}} = 3j$
Gambar di atas adalah gambar seluruh vektor posisi yang terdapat dalam soal. Sesuai gambar, berlaku:
$\Delta r = \vec{r_{1}}+ \vec{r_{2}}+ \vec{r_{3}}$
$\Delta r = -3i + 4i - 4j + 3j$
$\Delta r = (-3+4)i + (-4+3)j$
$\Delta r = i - j$
Maka besar perpindahan adalah:
$s = \sqrt{(\Delta r_{x})^{2}+(\Delta r_{y})^{2}}$
$s = \sqrt{1^{2} + (-1)^{2}}$
$\mathbf{s = \sqrt {2} \textup{ km}}$
///////////////////////////////////////////////////////arah perpindahan////////////////////////////////////////////////
Tinggal memakai rumus no. 3:
$\tan \theta = \frac{\Delta r_{y}}{\Delta r_{x}}$
$\tan \theta = \frac{1}{-1}$
$\tan \theta = -1$
$\mathbf {\theta = 315^{\circ}} \textup{(KUADRAN IV [360-45] karena x negatif)}$
Jangan lupa tinggalkan komen! ^_^
Referensi:
Widodo, Tri. Fisika untuk SMA/MA XI. Jakarta: Pusat Perbukuan, Departemen Pendidikan Nasional (BSE), 2009.
Kanginan, Marthen. SeribuPena FISIKA untuk SMA/MA Kelas XI. Jakarta: Erlangga. 2008



Buat contoh soal nomor 2 kan soalnya km ko pas diketahui posisi vektornya jadi meter
BalasHapus